COT et variantes de repères avancées expliquées

Base de connaissances sur l'IA1年前更新 Sharenet.ai

1.5K 0

Avertissement : Bien que les techniques de guidage de base (par exemple, zéro/peu d'exemples ou des conseils impératifs) soient très efficaces, des conseils plus sophistiqués peuvent être plus efficaces face à certaines énigmes complexes (par exemple, mathématiques/programmation ou problèmes nécessitant un raisonnement logique en plusieurs étapes). Étant donné que les grands modèles de langage (LLM) ont naturellement des difficultés à traiter de tels problèmes (leur pouvoir de raisonnement n'augmente pas de façon monotone avec la taille du modèle), la plupart des recherches sur la conception des messages-guides se sont concentrées sur la manière d'améliorer le raisonnement et la capacité à résoudre des problèmes complexes. Des indices simples suffisent pour la plupart des autres problèmes.

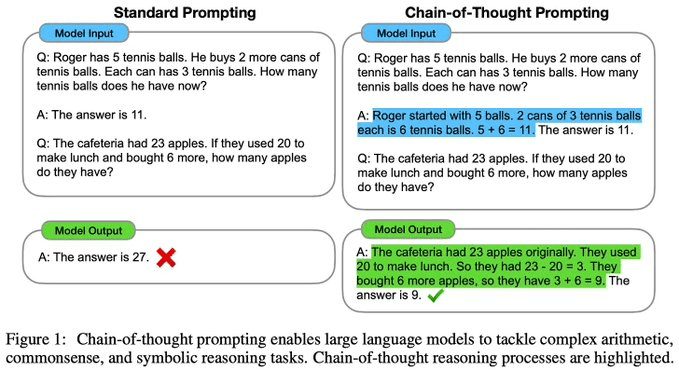
Chaîne de pensée (CoT)Hints [1] active les capacités de raisonnement de LLM en ajoutant une chaîne d'étapes de raisonnement intermédiaires aux hints du modèle. En ajoutant une chaîne de pensées pour chaque exemple, le modèle apprend (grâce à l'apprentissage contextuel) à générer automatiquement des chaînes de pensées similaires avant de donner une réponse. L'étude de [1] montre qu'expliquer explicitement le processus de raisonnement pour résoudre un problème peut en fait être efficace pour améliorer la capacité de raisonnement d'un modèle.

Entrée :
Les nombres impairs de cette série s'additionnent pour former un nombre pair : 4, 8, 9, 15, 12, 2, 1.
A : Additionnez tous les nombres impairs (9, 15, 1) pour obtenir 25. La réponse est Faux.
Les nombres impairs de ce groupe s'additionnent pour former un nombre pair : 17, 10, 19, 4, 8, 12, 24.
A : Additionnez tous les nombres impairs (17, 19) pour obtenir 36. La réponse est Vrai.
Les nombres impairs de cette série s'additionnent pour former un nombre pair : 16, 11, 14, 4, 8, 13, 24.
A : Additionnez tous les nombres impairs (11, 13) pour obtenir 24. La réponse est Vrai.
Les nombres impairs de cette série s'additionnent pour former un nombre pair : 17, 9, 10, 12, 13, 4, 2.
A : Additionnez tous les nombres impairs (17, 9, 13) pour obtenir 39. La réponse est Faux.
Les nombres impairs de cette série s'additionnent pour former un nombre pair : 15, 32, 5, 13, 82, 7, 1.
A :
Sortie :
Additionnez tous les nombres impairs (15, 5, 13, 7, 1) pour obtenir 41. la réponse est Faux.

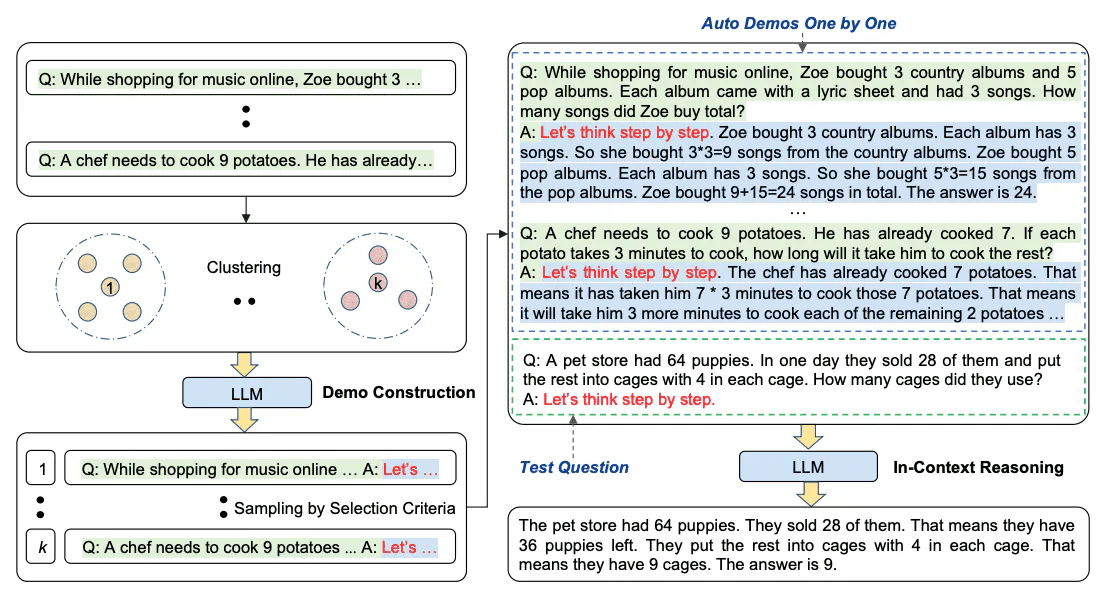
Chaîne de pensée automatisée (Auto-CoT)[8] : Lors de l'utilisation de chaînes de pensée, le processus nécessite la création manuelle d'exemples efficaces et diversifiés. Ce travail manuel peut conduire à des solutions sous-optimales. [8] propose un moyen d'éliminer l'effort manuel en utilisant les invites "Let's think step by step" des LLM pour générer des chaînes de raisonnement l'une après l'autre. Ce processus automatisé peut toujours produire des erreurs dans les chaînes générées. Pour atténuer les effets des erreurs, il est important de varier la présentation. Ce travail propose Auto-CoT, qui échantillonne les problèmes avec diversité et génère des chaînes de raisonnement pour construire des démonstrations.

L'Auto-CoT se compose de deux phases principales :

Étape 1 : Regroupement des problèmes : diviser le problème donné en plusieurs groupes.
Étape 2 : Échantillonnage de démonstration : sélectionner un problème représentatif de chaque réseau et générer sa chaîne d'inférence en utilisant Zero-Shot-CoT avec une heuristique simple.
Des heuristiques simples peuvent être la longueur du problème (par exemple, 60 tokens) et le nombre d'étapes du raisonnement (par exemple, 5 étapes d'inférence). Cela encourage les modèles à utiliser des présentations simples et précises.

Le processus est illustré ci-dessous :

Variante du CdTLa validité des messages-guides de la CdT et leur popularité ont conduit à la proposition de plusieurs techniques dérivées :

Zéro exemple CoT [2] : supprime quelques exemples et incite le modèle à générer un raisonnement logique pour résoudre le problème en ajoutant "Réfléchissons étape par étape" à la fin de l'invite. L'invite est complétée par la phrase "Réfléchissons étape par étape", qui incite le modèle à générer un raisonnement logique pour résoudre le problème.

Entrée :
Je suis allé au marché et j'ai acheté 10 pommes. J'ai donné 2 pommes à mon voisin et 2 pommes au réparateur. Ensuite, je suis allé acheter 5 pommes et j'en ai mangé 1. Combien de pommes me reste-t-il ?
Réfléchissons étape par étape.
Sortie :
Tout d'abord, vous commencez avec 10 pommes.
Vous avez donné 2 pommes à votre voisin et au réparateur, il vous reste donc 6 pommes.
Vous achetez ensuite 5 pommes, ce qui fait que vous avez maintenant 11 pommes.
À la fin, vous avez mangé 1 pomme, il vous reste donc 10 pommes.

Autoconsistance (SC) [3] : améliore la robustesse du processus de raisonnement en générant indépendamment plusieurs solutions et en votant à la majorité sur la réponse finale.

Entrée :
Q : Il y a 15 arbres dans la forêt. Des ouvriers forestiers vont planter des arbres dans la forêt aujourd'hui. Lorsqu'ils auront terminé, il y aura 21 arbres. Combien d'arbres les forestiers ont-ils plantés aujourd'hui ?
R : Nous avons commencé avec 15 arbres. Plus tard, nous avons eu 21 arbres. La différence doit être le nombre d'arbres qu'ils ont plantés. Ils ont donc dû planter 21-15 = 6 arbres. La réponse est 6.
Q : Il y avait trois voitures dans le parking et deux autres voitures sont arrivées, combien de voitures y avait-il dans le parking ?
R : Il y a déjà 3 voitures dans le parking. Deux autres voitures sont arrivées. Il y a maintenant 3 + 2 = 5 voitures. La réponse est 5.
Q : Leah a 32 morceaux de chocolat et sa sœur en a 42. Si elles ont mangé 35 pièces, combien leur reste-t-il de pièces au total ?
A : Léa a 32 chocolats et la sœur de Léa en a 42. Cela signifie qu'au départ, il y avait 32 + 42 = 74 chocolats. 35 chocolats ont déjà été mangés. Il leur reste donc un total de 74 - 35 = 39 chocolats. La réponse est 39.
Q : Jason a 20 sucettes. Il donne quelques sucettes à Denny. Maintenant, Jason n'a plus que 12 sucettes. Combien de sucettes Jason a-t-il donné à Denny ?
A : Jason a 20 sucettes. Comme il n'en a plus que 12, il doit donner le reste à Denny. Le nombre de sucettes qu'il donne à Denny doit être 20 - 12 = 8 sucettes. La réponse est 8.
Q : Shawn a cinq jouets. Pour Noël, il a reçu deux jouets de ses parents. Combien de jouets a-t-il maintenant ?
A : Il a 5 jouets. Il en a reçu 2 de sa mère, ce qui fait qu'il a 5 + 2 = 7 jouets. Ensuite, il a reçu 2 jouets de son père, ce qui fait qu'au total, il a 7 + 2 = 9 jouets. La réponse est 9.
Q : La salle des serveurs compte 9 ordinateurs. Du lundi au jeudi, 5 ordinateurs sont installés chaque jour. Combien y a-t-il d'ordinateurs dans la salle des serveurs ?
R : Il y a eu 4 jours, du lundi au jeudi. Chaque jour, 5 ordinateurs ont été ajoutés. Cela signifie qu'un total de 4 * 5 =
20 ordinateurs. Il y avait 9 ordinateurs au début, il y a donc maintenant 9 + 20 = 29 ordinateurs. La réponse est 29.
Q : Michael possède 58 balles de golf. Mardi, il a perdu 23 balles de golf. Mercredi, il en a perdu 2 de plus. Combien de balles de golf lui restait-il à la fin de la journée de mercredi ?
R : Michael avait initialement 58 balles. Le mardi, il en a perdu 23, ce qui fait qu'il avait 58-23 = 35 boules. Mercredi, il en a perdu 2 de plus, ce qui fait qu'il a maintenant 35-2 = 33 boules. La réponse est 33.
Q : Olivia dispose de 23 $. Elle a acheté cinq bagels pour 3 $ chacun. Combien d'argent lui reste-t-il ?
A : Elle a acheté 5 bagels pour 3 $ chacun. Cela signifie qu'elle a dépensé 15 dollars. Il lui reste 8 $.
Q : Quand j'avais 6 ans, ma sœur avait la moitié de mon âge. Maintenant que j'ai 70 ans, quel âge a ma sœur ?
A :
Sortie 1 :
Lorsque j'avais 6 ans, ma sœur avait la moitié de mon âge, soit 3 ans. Aujourd'hui, j'ai 70 ans, donc elle a 70-3 = 67 ans. La réponse est 67.
Sortie 2 :
Lorsque le narrateur avait 6 ans, sa soeur avait la moitié de son âge, soit 3 ans. Maintenant que le narrateur a 70 ans, sa sœur aurait 70-3 = 67. La réponse est 67.
Sortie 3 :
Quand j'avais 6 ans, ma sœur avait la moitié de mon âge, soit 3 ans. Aujourd'hui, j'ai 70 ans, donc elle a 70/2 = 35 ans. La réponse est donc 35.

Least-to-Most [4] : décomposer le problème en plusieurs parties, les résoudre une par une, puis utiliser la réponse à chaque sous-problème comme contexte pour résoudre le suivant.

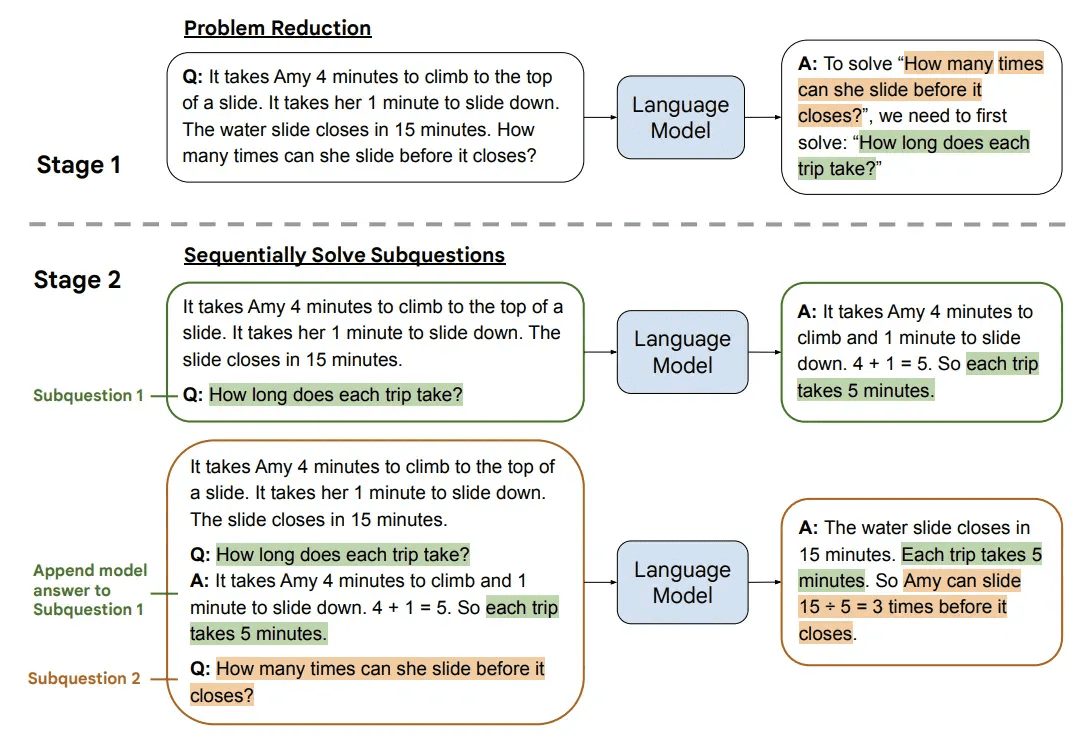
Entrée :
Demande de renseignements des clients.
J'ai acheté un t-shirt de votre collection Arnold le 1er mars. J'ai vu qu'il était en promotion et j'ai donc acheté un t-shirt qui était à l'origine en réduction de 30 $. J'ai remarqué que vous aviez maintenant une nouvelle réduction sur les t-shirts, 50%. Je me demandais si je pouvais le retourner et avoir encore assez de crédit en magasin pour acheter deux de vos t-shirts ?
Commandement.
Vous êtes un représentant du service clientèle chargé de répondre aux demandes des clients de manière amicale. Les retours sont autorisés dans un délai de 30 jours. Nous sommes le 29 mars. Toutes les chemises bénéficient actuellement d'un rabais de 50%. Les prix de vos chemises en magasin varient entre 18 et 100 dollars. Veuillez ne pas inventer d'informations sur la politique de réduction.
Quelles sont les sous-questions à traiter avant de pouvoir répondre à cette question ?
Sortie :
1. la date à laquelle le client a acheté la chemise ;
2. l'activité d'escompte actuelle ;
3. gamme de prix des chemises dans la boutique ;
4. si le client dispose d'un crédit commercial suffisant ;
5. la politique de retour des clients.
Entrée :
Demande de renseignements des clients.
J'ai acheté un t-shirt de votre collection Arnold le 1er mars. J'ai vu qu'il était en promotion et j'ai donc acheté un t-shirt qui était à l'origine en réduction de 30 $. J'ai remarqué que vous aviez maintenant une nouvelle réduction sur les t-shirts, 50%. Je me demandais si je pouvais le retourner et avoir encore assez de crédit en magasin pour acheter deux de vos t-shirts ?
Commandement.
Vous êtes un représentant du service clientèle chargé de répondre aux demandes des clients de manière amicale. Les retours sont autorisés dans un délai de 30 jours. Nous sommes le 29 mars. Toutes les chemises bénéficient actuellement d'un rabais de 50%. Les prix de vos chemises en magasin varient entre 18 et 100 dollars. Veuillez ne pas inventer d'informations sur la politique de réduction.
Déterminez si le client se trouve dans la période de retour de 30 jours. Procédons étape par étape.
Sortie :
Cher client, Nous vous remercions de votre soutien à la gamme Arnold ! Nous sommes heureux de vous offrir nos services. Notre politique de retour est que les clients peuvent retourner les articles dans les 30 jours suivant l'achat. Comme vous avez acheté votre article le 1er mars, vous êtes encore dans la période de retour et vous pouvez le retourner.
En outre, nous organisons actuellement une vente 50% au cours de laquelle vous pouvez utiliser votre crédit pour acheter deux t-shirts de la collection Arnold. Nos t-shirts vont de 18 à 100 dollars, ce qui vous permet de choisir celui qui correspond le mieux à vos besoins.
Si vous avez d'autres questions, n'hésitez pas à nous contacter. Nous serons heureux de vous servir !

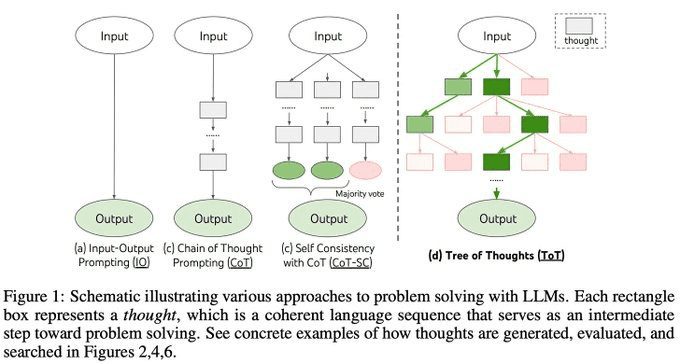
L'arbre des pensées [ToT].Conseil [5] : les conseils CoT ne résolvent pas les problèmes qui nécessitent une planification, une anticipation stratégique, un retour en arrière et l'exploration de plusieurs solutions en parallèle. Les conseils toT divisent les problèmes complexes en une série de problèmes plus simples (ou "pensées"). lLM génère de nombreuses "pensées" et évalue en permanence leur progression vers une solution finale par le biais du langage naturel. LLM génère de nombreuses "pensées" et évalue en permanence leur progression vers la solution finale en langage naturel. En utilisant l'auto-évaluation par le modèle de la progression de la solution, nous pouvons appliquer des algorithmes de recherche largement utilisés (par exemple, la recherche en largeur d'abord ou en profondeur d'abord) pour faciliter le processus d'exploration et permettre la prévoyance/le retour en arrière lors de la résolution de problèmes.

Supposons que trois experts différents répondent à cette question.
Tous les experts ont écrit les premières étapes de leur réflexion sur la question et les ont ensuite partagées avec le groupe.
Tous les experts rédigent ensuite les prochaines étapes de leur réflexion et les partagent.
Et ainsi de suite jusqu'à ce que tous les experts aient décrit toutes les étapes de leur réflexion.
Dès que l'on s'aperçoit que les démarches d'un expert sont erronées, il faut s'en séparer.
Excusez-moi...

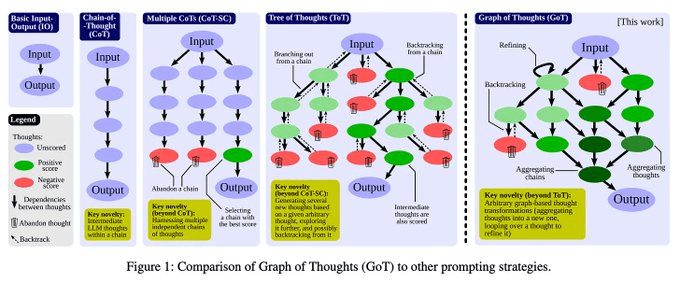
Graphique des pensées (GoT)Indices [6, 7] : des recherches ultérieures ont permis d'étendre les travaux sur les indices de la FdT aux stratégies de raisonnement basées sur les graphes. Ces techniques sont similaires aux indices de la ToT, mais ne supposent pas que le cheminement de la pensée qui génère une solution soit linéaire. Nous pouvons réutiliser les pensées et même les appliquer de manière récursive à une série de pensées lors de l'élaboration d'une solution. Bien qu'une variété de stratégies d'indication basées sur les graphes ait été proposée, ces techniques, ainsi que les indications ToT, ont été critiquées pour leur manque d'utilité. La résolution d'un problème de raisonnement à l'aide d'indices GoT peut exiger du LLM qu'il effectue un grand nombre d'étapes de raisonnement !

Vous trouverez ci-dessous des liens vers tous les documents cités ci-dessus !

[1] https://arxiv.org/abs/2201.11903
[2] https://arxiv.org/abs/2205.11916
[3] https://arxiv.org/abs/2203.11171
[4] https://arxiv.org/abs/2205.10625
[5] https://arxiv.org/abs/2305.10601
[6] https://arxiv.org/abs/2308.09687
[7] https://arxiv.org/abs/2305.16582

[8] https://arxiv.org/abs/2201.11903